A Meet FLEET innovation-and-industry event poster
Karen Livesey, FLEET Associate Scientific Investigator, University of Newcastle
The Challenge
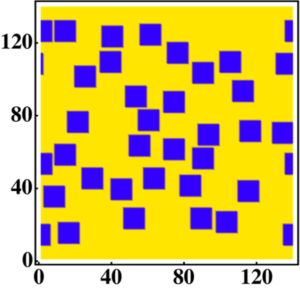
Figure 1: An example two-dimensional slice of an electromagnetic metamaterial made up of magnetic inclusions (blue squares) in a nonmagnetic host material (yellow). In this case, the inclusions occupy 25% of the total volume.
Metamaterials = artificial structures with properties that do not occur in nature.
They are used to make electromagnetic absorbers and communication devices at microwave, infrared and optical frequencies.
A way to accurately predict electromagnetic properties of metamaterials is needed.
Predicting metamaterials’ effective or average permeability has been a challenge for over a century. Analytic methods are only accurate for low-volume fractions of magnetic inclusions.
The Solution
We developed a numerical calculation method for the effective magnetic permeability tensor of composites, based on Gauss’ law.
Key Benefits
- Calculation is not limited to low-volume fractions of inclusions (blue squares in Figure 1)
- Any magnetic inclusion shape and microscopic arrangement can be considered
- Valid at high frequencies (GHz or THz)
Development Stage
- Initial method developed
- Seeking strategic partners
Brief Description & Differentiation
-
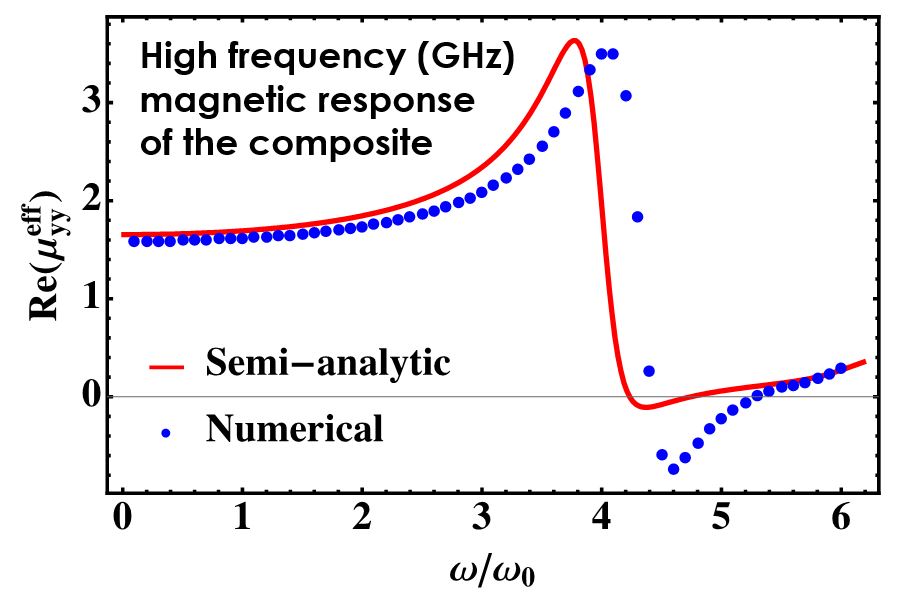
Figure 2: The predicted high frequency magnetic permeability of the composite shown in Figure 1, as a function of GHz frequency. There is a peak near ferromagnetic resonance. Our method (dots) is more accurate than conventional semi-analytic methods (line).
The composite material is broken up into a grid of computational sites
- Maxwell’s equations are re-written using finite difference methods for the derivatives
- The resulting set of linear equations is solved to find the magnetic fields at all grid sites
- These fields are averaged in order to find the effective permeability tensor.
- Many methods to calculate the permeability tensor ignore the coupling between different tensor components, whereas this method does not, resulting in greater accuracy.
- Any inclusion shape or configuration – not just randomly placed – can be treated
- Unlike for analytic expressions, inclusions need not be dilute, uniformly distributed, nor of some regular shape
Intellectual Property
No patent
Key Publications
- R.E. Camley, A.L. Carpenter and K.L. Livesey, Physical Review Applied in press (2023)
More information
- Contact Dr Karen Livesey, University of Newcastle, NSW karen.livesey@newcastle.edu.au